logoMathBits.comTable of Contents

Solving Exponential Expressions (ln and e)
Many exponential expressions can be quickly solved on the home screen.
 

 
 
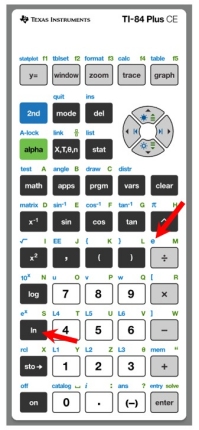
Start by finding the keys you will be using:
     e (to the first power) can be found above the division key.
    
     ln has its own key on the left side of the keypad.  Border
     ex is found above the ln key.


Remember: e is an irrational number, approximately 2.71828183, named after the 18th century Swiss mathematician, Leonhard Euler.

 f (x) = ex,  is called the natural exponential function.
 f (x) = ln x, is called the natural logarithmic function.
These two functions are inverses of one another.

When composed, these two functions return the starting value,
thus creating the identity function, y = x.
1.   1
Notice how the calculator automatically forces the use of the parentheses.  Get in the habit of closing the parentheses.
• The first entry uses the e value above the division key. The exponent of 1 is implied.
• The second entry uses the e x above the ln key.  Notice how this second entry illustrates the composition of the two inverse functions ln and ex, returning the starting value of 1.
Answer: 1


Be sure to move "down" from the 1
to close the parentheses. Don't close
the parentheses up next to the 1.

2.   3

Simply enter the expression on the home screen.  Again, notice the composition of functions at work on the two inverse functions. The original starting value for x (which is 4) is returned from the composition.
Answer: 4

3.  5

Again, simply enter the expression on the home screen.  Did you notice that this is NOT a composition of the two inverse functions?  The "2" is in the way.

Of course, the problem could be rewritten using properties of logs to utilize the composition of the inverses:  44
Answer: 9

4.  7

The "store" command was entered first just to demonstrate that this calculator is holding a "7" in x. When you type in this problem, your answer will be whatever YOUR calculator had stored in x. Your calculator most likely shows a different value. 
The thing to notice is that it returns what ever value represents x, thus telling us that 55, which we can verify from the composition of these inverse functions. 
Answer: x

 


divider
Finding Your Way Around TABLE of CONTENTS